#include <bits/stdc++.h>
using namespace std;

const int N = 31;

long long f[N][N][N][N][N];
int n;
int s[N];

int main() {
    while(scanf("%d", &n), n) {
        memset(s, 0, sizeof s);
        for(int i = 1; i <= n; i ++ ) scanf("%d", &s[i]);
        memset(f, 0, sizeof f);
        f[0][0][0][0][0] = 1;
        for(int a = 0; a <= s[1]; a ++ ) 
            for(int b = 0; b <= min(a, s[2]); b ++ ) 
                for(int c = 0; c <= min(b, s[3]); c ++ )    
                    for(int d = 0; d <= min(c, s[4]); d ++ )    
                        for(int e = 0; e <= min(d, s[5]); e ++ ) {
                            long long &val = f[a][b][c][d][e];
                            if(a && a - 1 >= b) val += f[a - 1][b][c][d][e];
                            if(b && b - 1 >= c) val += f[a][b - 1][c][d][e];
                            if(c && c - 1 >= d) val += f[a][b][c - 1][d][e];
                            if(d && d - 1 >= e) val += f[a][b][c][d - 1][e];
                            if(e) val += f[a][b][c][d][e - 1];
                        }
        cout << f[s[1]][s[2]][s[3]][s[4]][s[5]] << '\n';
    }
    return 0;
}

通过题目我们可以知道，题目要求的是从前到后考虑前是指从1~N我们需要考虑的是从前向后递增（身高递增）的然后从左到右也是递增的（因为第一排的人数最多，从最后一排的视角来看就是递增的）

然后我们在去考虑人数，设第一排存放$a_1$个人，第二排$a_2$，依次类推到第五排$a_5$（因为题目说了最多就到5）

那么则有$a_1≥a_2≥a_3≥a_4≥a_5$所以我们在考虑方案的时候也不能忽略这个因素，假设考虑任意的可能存在的方案我们已经放好了$x$个人（这$x$个人全部合法放置也就是满足题目条件的放置这样递增的放置）如图所示

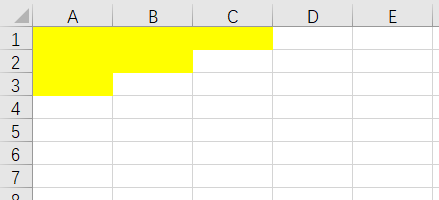
用excel来的代替一下比较直观，黄色的是已经放好的人，我们假设这里放了身高为1，2，3，4，5，6身高的人我们先不去考虑怎么放置的，下一步要放置的身高我们假设为7，7身高的学生我们放置的位置只可能有这么几种选择

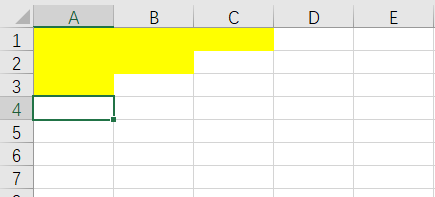
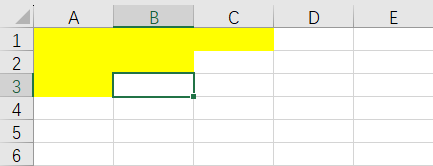
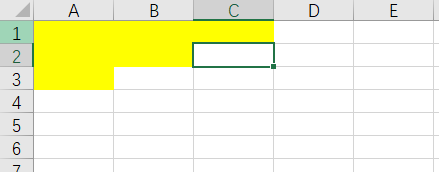
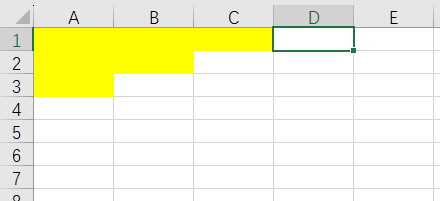
即鼠标光标的位置，我们会发现没有别的位置可以放置了

我们可以发现，我们对于已有的方案来说我们并不关心我们怎么摆放完成的，什么意思呢，就是我们不关心摆放的具体方案，并且这个方案合不合法，在简而言之就是我们只关心的是抽象的，也就是摆放的轮廓，如何摆放，和我们没有和本题没有任何关系于是我们可以用一个函数f(a, b, c, d, e) 这样的函数来表示我们本题的方案，代表什么意思呢，代表第一排放了a人，第二排放了b人，第三排c人，第四排d人，第五排e人，这的一个5元函数来表示出当前方案放置了多少人

并且我们可以发现，我们用这样的方式来表述了以后，我们可以很清楚的知道，对于当前的方案的轮廓是一个怎么样的一回事，如果题目给定的k < 5那么多出的这些位置直接是0即可，代表不放人我们算的时候不去考虑就可以了

那讲了这么多也没有说究竟要这么计算方案，方案的计算如下：

我们可以由于题目的表述我们可以发现其实f(0, 0, 0, 0, 0)也是一种合法方案，因为他代表了第一排0，二排0，三排0, 四排0，五排0的一种方案他和题目表述的并冲突所以f(0, 0, 0, 0, 0) = 1通过题目我们知道第一排人数的需要大于等于第二排以后的所有的人数，第二排以需要大于等于第三排以后以此类推

那么我考虑当前方案，f(a, b, c, d, e)则有考虑满足条件我们已经拿一个人放到第一排人数a，他的人数放的时候必须要大于等于b，那放的是什么时候呢，那就是a-1>=b，当然我a-1的时候不能小于0 那么条件就是if(a && a - 1 >= b)然后我们是从f(a - 1, b, c, d, e)放了一个人,所以f(a - 1, b, c, d, e, d)所有的方案构成了f(a, b, c, d, e) 方案的集合中的方案的一部分则有f(a, b, c, d, e) += f(a - 1, b, c, d, e)

其他的方案就不再赘述，思考方式和前面一样，放一下代码块

int &val = f[a][b][c][d][e];
if(a && a - 1 >= b) val += f[a - 1][b][c][d][e];
if(b && b - 1 >= c) val += f[a][b - 1][c][d][e];
if(c && c - 1 >= d) val += f[a][b][c - 1][d][e];
if(d && d - 1 >= e) val += f[a][b][c][d - 1][e];
if(e) val += f[a][b][c][d][e - 1];

N[i]是每一排的最多可以放置的人数

然后我们依次去考虑a <= N[1], b <= min(a, N[2]), c <= min(b, N[3]), d <= min(c, N[4], e <= min(d, N[5]) 如此限制下的每一个方案，通过每一个方案算，最终可以算出最后的方案 f(N[1], N[2], N[3], N[4], N[5])，所以方案f(N[1], N[2], N[3], N[4], N[5])即为所求